Data

In the data, through the observations fusion of multiple types or of multiple constellations, we use the characteristics of detection height, time and spatial resolution of different data as showed in Figure 1 to combine with each other to achieve the construction of the accurate ionosphere.

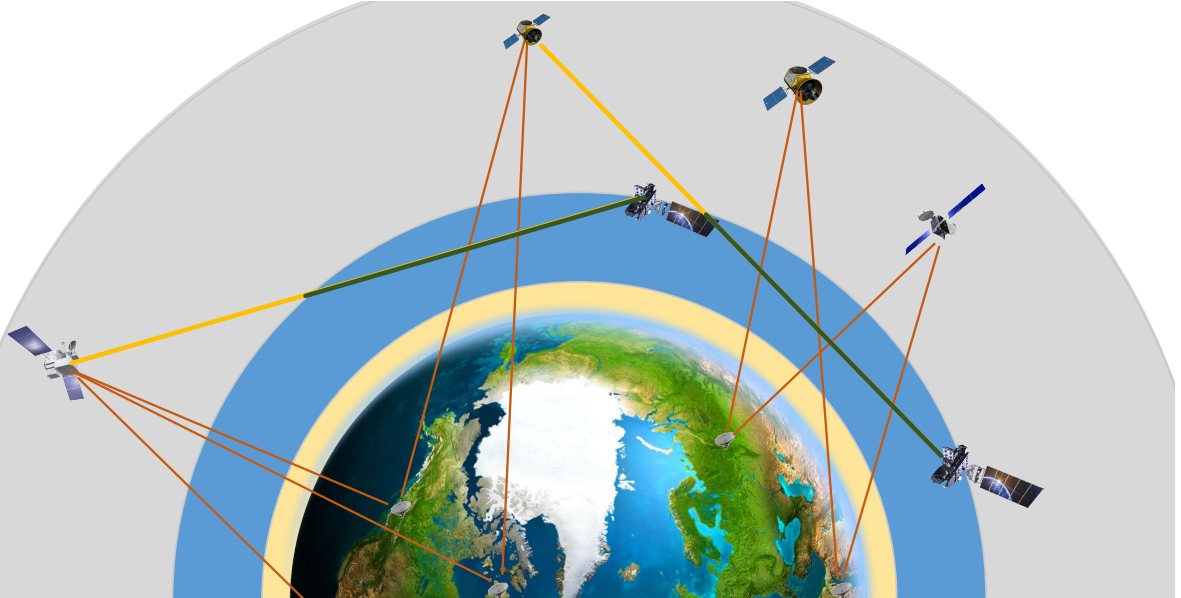Figure 1. Multiobserving systems: green line, signal path across bottom region of the ionosphere 800km during occultation; yellow line, signal path across the top region during occultation; orange line, signal path across the ionosphere of ground-based GNSS observation.

Method

Through ionospheric observations (occultation observations, ground-based GNSS observations, and GNSS-LEO top region observations), we have developed three methods for ionospheric modeling. (1) GIM model data based on a spherical harmonic function assumed by a single layer. (2) The ionPrf data (Electron Density Profiles of the ionosphere) formed based on Abel inversion with local spherical symmetry. (3) The ionospheric assimilation model based on the KF algorithm with the ionospheric empirical model as the background field.

Errors

Various errors and influences in the inversion of the ionospheric data, especially easily overlooked errors, were analyzed,and corresponding improvement methods were proposed. From the statistics of vertical TEC and electron density deviations and RMSE( Root mean square of errpr ), after correcting the observed data, the assimilation results are significantly improved, which confirmed the effectiveness of the correction algorithm. These errors should be reduced before processing,and the time/grid correction can effectively and steadily improve the assimilation accuracy.

The DCBs of receivers and transmitters

The Center for Orbit Determination in Europe (CODE) and other research institutes obtain the solution DCB based on the single-layer ionospheric hypothesis; however, the top region of the ionosphere is affected by magnetic storms and possesses a complex spatial environment. The resulting errors are transmitted mainly to the absolute slant total electron content (STEC). The root mean square (RMS) DCBs of GNSS stations solved by the CODE/IGS institutions and the DCBs of the GPS/LEO observations in the podTec data from COSMIC used to estimate the errors of the DCBs were added to the background field of the ionosphere to obtain the STEC error. Accordingly, the STEC error was suppressed during assimilation.

The following observational equation was employed for additional electron density observations:

$\begin{bmatrix}h_{i,j}&\delta^T_i&\delta^R_i \\ \delta_{k,j}&O&O\end{bmatrix}\begin{bmatrix}ne_j \\ \Delta DCB^T \\ \Delta DCB^R\end{bmatrix}=\begin{bmatrix}{STEC}_i \\ ne_k \end{bmatrix}$

where $h_{i,j}$ is the projection matrix obtained by ray tracing for ground-based/spaceborne observations; $\delta^T_i$,$\delta^R_i$ are the DCB coefficients of the transmitters and receivers; $\delta_{k,j}$ is the coefficient of the $j$th grid for the $k$th electron density observation data point; $NE_j$ is the electron density of the $j$ grid; $\Delta DCB^T, \Delta DCB^R$are the assimilated DCB differences between the DCBs of the transmitters and receivers and the CODE transmitter and receiver DCBs, respectively; and $STEC_j, NE_k$ are the observed STEC values obtained through the CODE/IGS products and the electron densities, respectively.

If the model error, DCBs error, and the error of electron density observation data as it was introduced during the assimilation process were determined, we can obtain the ionospheric update equation considering the effects of DCBs.